
If a function f is not bijective, inverse function of f cannot be defined.For onto function, range and co-domain are equal.one to one function never assigns the same value to two different domain elements.A function is one to one if it is either strictly increasing or strictly decreasing.If f and fog are onto, then it is not necessary that g is also onto.If f and fog both are one to one function, then g is also one to one. If both X and Y are limited with the same number of elements, then f: X Y is one-one, if and only if f is surjective or onto function.If f and g both are onto function, then fog is also onto.If f and g both are one to one function, then fog is also one to one.A function f is decreasing if f(x) ≤ f(y) when x f(y) when x>y. It is a function which assigns to b, a unique element a such that f(a) = b. The inverse of bijection f is denoted as f -1. Inverse Functions:Bijection function are also known as invertible function because they have inverse function property.One to one correspondence function(Bijective/Invertible): A function is Bijective function if it is both one to one and onto function.It is not required that a is unique The function f may map one or more elements of A to the same element of B. Onto Function (surjective): If every element b in B has a corresponding element a in A such that f(a) = b.We can express that f is one-to-one using quantifiers as or equivalently, where the universe of discourse is the domain of the function. It never maps distinct elements of its domain to the same element of its co-domain. One to one function(Injective): A function is called one to one if for all elements a and b in A, if f(a) = f(b),then it must be the case that a = b.Mathematics | Rings, Integral domains and Fields.Mathematics | Independent Sets, Covering and Matching.
ONTO VS ONE TO ONE GRAPH SERIES
Mathematics | Sequence, Series and Summations.  Mathematics | Generating Functions – Set 2. Discrete Maths | Generating Functions-Introduction and Prerequisites. Mathematics | Total number of possible functions. Mathematics | Classes (Injective, surjective, Bijective) of Functions. Number of possible Equivalence Relations on a finite set. Mathematics | Closure of Relations and Equivalence Relations. Mathematics | Representations of Matrices and Graphs in Relations. it only means that no y -value can be mapped twice. this means that in a one-to-one function, not every x -value in the domain must be mapped on the graph. in a one-to-one function, every y -value is mapped to at most one x - value. Discrete Mathematics | Representing Relations Explanation: in an 'onto' function, every x -value is mapped to a y value. Mathematics | Introduction and types of Relations. Mathematics | Partial Orders and Lattices. Mathematics | Power Set and its Properties. Inclusion-Exclusion and its various Applications.
Mathematics | Generating Functions – Set 2. Discrete Maths | Generating Functions-Introduction and Prerequisites. Mathematics | Total number of possible functions. Mathematics | Classes (Injective, surjective, Bijective) of Functions. Number of possible Equivalence Relations on a finite set. Mathematics | Closure of Relations and Equivalence Relations. Mathematics | Representations of Matrices and Graphs in Relations. it only means that no y -value can be mapped twice. this means that in a one-to-one function, not every x -value in the domain must be mapped on the graph. in a one-to-one function, every y -value is mapped to at most one x - value. Discrete Mathematics | Representing Relations Explanation: in an 'onto' function, every x -value is mapped to a y value. Mathematics | Introduction and types of Relations. Mathematics | Partial Orders and Lattices. Mathematics | Power Set and its Properties. Inclusion-Exclusion and its various Applications. 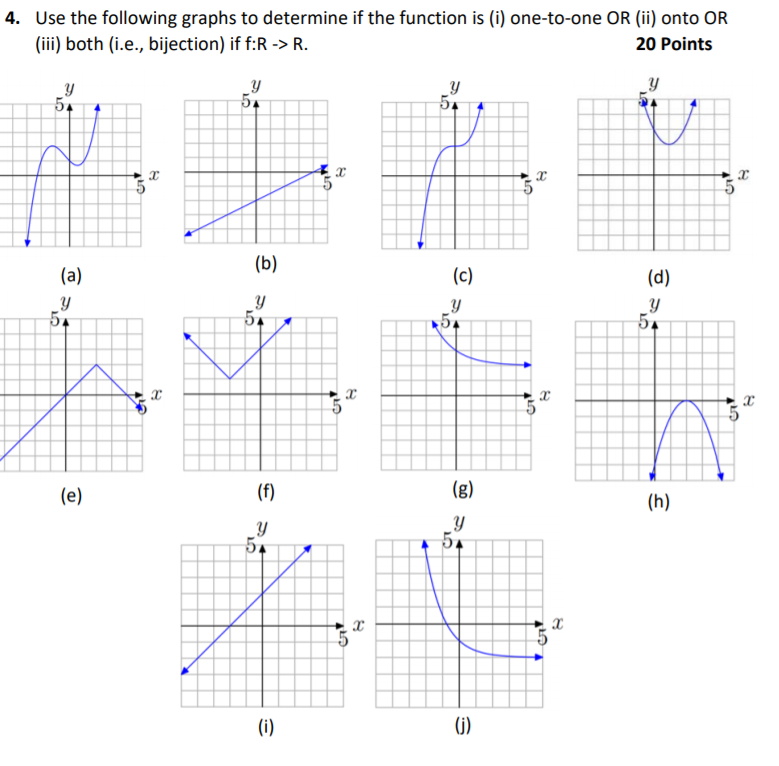 Mathematics | Set Operations (Set theory).
Mathematics | Set Operations (Set theory). 
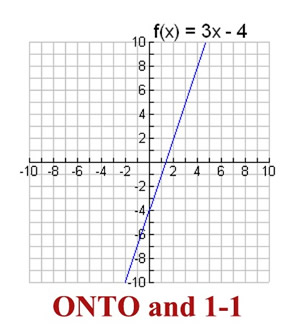
Mathematics | Introduction of Set theory.ISRO CS Syllabus for Scientist/Engineer Exam.ISRO CS Original Papers and Official Keys.GATE CS Original Papers and Official Keys.The mapping of 'f' is said to be onto if every element of Y is the f-image of at least one element of X. => f Y that is range is not a proper subset of co-domain. Mapping (when a function is represented using Venn-diagrams then it is called mapping), defined between sets X and Y such that Y has at least one element 'y' which is not the f-image of X are called into mappings. One-to-one mapping is called injection (or injective). Graphically, if a line parallel to x axis cuts the graph of f(x) at more than one point then f(x) is many-to-one function and if a line parallel to y-axis cuts the graph at more than one place, then it is not a function. While x → x 2, x ε R is many-to-one function.
no two elements of A have the same image in B), then f is said to be one-one function. If for each x ε A there exist only one image y ε B and each y ε B has a unique pre-image x ε A (i.e. Consider the function x → f(x) = y with the domain A and co-domain B.
IIT JEE Coaching For Foundation Classesįunctions can be classified according to their images and pre-images relationships. Structural Organisation in Plants and Animals.








 0 kommentar(er)
0 kommentar(er)
